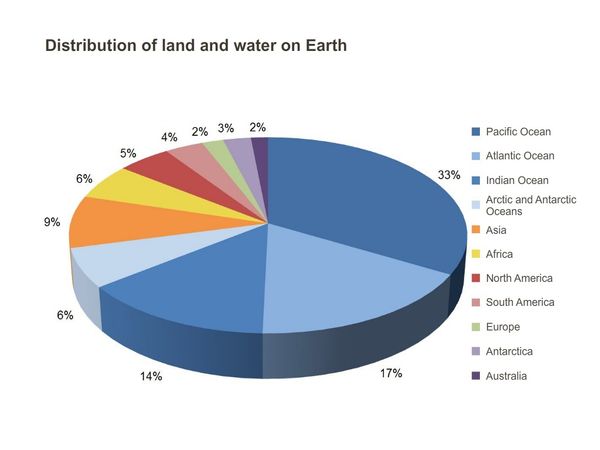
It is estimated that the Earth has a total volume of 1.386 billion km³ (333 million cubic miles) of water. However, over 97% of the water on earth is saline or seawater, with an average salinity of 35‰ (or 4.5%, roughly equivalent to 34gm of salts in 1kg of seawater). Typically, fresh water is defined as water with a salinity of less than 1 percent that of the oceans – i.e. below around 0.35‰. Of the barely 2.5–2.75% fresh water of the total available water on earth, 1.75–2% is frozen in glaciers, ice and snow, 0.5–0.75% is available as fresh groundwater and soil moisture, and less than 0.01% of it is available as surface water in lakes, swamps and rivers. This <1% usable freshwater is very unevenly distributed across the Earth. For example, freshwater lakes contain 87% of the fresh surface water. Around 25% of it is in African great lakes, 22% in Lake Baikal in Russia and 21% in North American great lakes. Of these lakes, many are in locations inaccessible and inhospitable to humans.

Uneven distribution is also seen in the surface water available in rivers. Rivers and basins are often compared not according to their static volume, but to their flow of water, or surface runoff. Around 60% of this is distributed in Asia and South America, whereas Australia accounts for only 1% of the river water resources. Even within continents, there are huge variations in river water availability. In fact, there is much more freshwater stored in the ground than what is avilable on the surface.

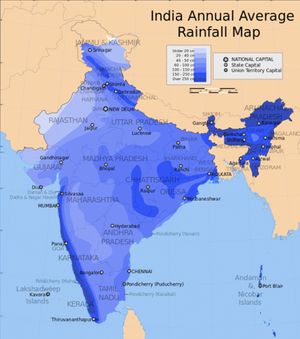
We can see the average rainfall map below to note how uneven rainfall is within a geographic region. India is one of the countries with a high amount of annual precipitation, but even here we can see arid areas.